Verification, Validation, and Uncertainty Quantification are critical pieces of simulation-based engineering workflows necessary to build confidence that computational results are relevant and reliable in the real world.
Verification checks that the simulation code is correct (e.g. it is solving the equations correctly), validation confirms that the simulation model accurately represents the real world (e.g. the equations being solved represent reality with sufficient fidelity), and uncertainty quantification assesses the reliability of the simulation results (e.g. how do the solutions change given the uncertainties in the computational and physical systems).
SmartUQ has a number of tools to help with the VVUQ process including dedicated DOEs for simulation and physical systems, multiple calibration methods, statistical comparisons, and a full UQ suite.
Verification focuses on ensuring that the simulation implementation is correct. Is this way it is very much in line with other software verification processes and key activities include:
Uncertainty quantification involves identifying, quantifying, and propagating uncertainties in simulation inputs, parameters, and models to assess their impact on the simulation outputs. For VVUQ workflows, some Key activities include:
This high level overview briefly explains where uncertainty comes from and what uncertainty quantification is.
Uncertainty Quantification (UQ) is the science of quantifying, characterizing, tracing, and managing uncertainty in computational and real world systems.
UQ seeks to address the problems associated with incorporating real world variability and probabilistic behavior into engineering and systems analysis. Simulations and tests answer the question: What will happen when the system is subjected to a single set of inputs? UQ expands on this question and asks: What is likely to happen when the system is subjected to a range of uncertain and variable inputs?
UQ started at the intersection of mathematics, statistics, and engineering. Drawing from these diverse fields has resulted in a set of system agnostic capabilities which require no knowledge of the inner workings of the system being studied. These powerful UQ methods only require information about the input/output response behavior. Thus, a method that works on an engineering system may be equally applicable to a financial problem that exhibits similar behavior. This allows many industries to benefit from advances in UQ.
UQ methods are rapidly being adopted by engineers and modeling professionals across a wide range of industries because they can answer many questions that were previously unanswerable. These methods make it possible to:
As computational power has increased and simulations and testing have become more sophisticated, it has become possible to make accurate predictions for more real world systems. Now the competitive frontier of engineering design has moved on to quickly predicting the behaviors of these systems when subjected to uncertain inputs. Monte Carlo based methods require generating and evaluating large numbers of system variations. These methods become prohibitive to use for large-scale problems. More recent methods, such as those incorporated in SmartUQ, have made UQ easier for small systems and actually feasible for large ones. There's never been a better time to start including uncertainty in your engineering process.
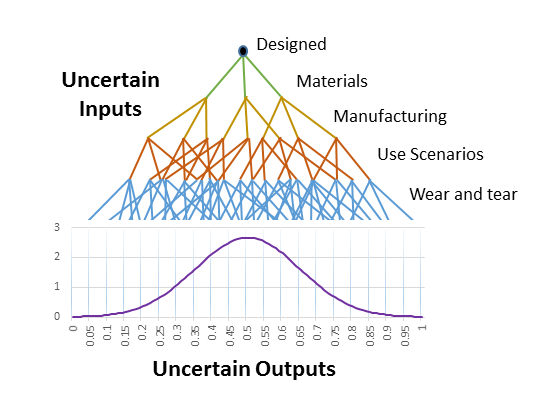Figure 1: How Uncertainty ArisesUncertainty is an inherent part of the real world. No two physical experiments ever produce exactly the same output values and many relevant inputs may be unknown or unmeasurable. Uncertainty effects almost all aspects of engineering modeling and design. Engineers have long dealt with measurement errors, uncertain material properties, and unknown design demand profiles by including factors of safety and extensively testing designs. By more deeply understanding and quantifying the sources of uncertainty, we can make better decisions with known levels of confidence.
Uncertainties are broadly classified into two categories: aleatoric and epistemic.
Aleatoric
Aleatoric uncertainty is uncertainty that is beyond our current ability to reduce by collecting more information. Thus, it may be considered inherent in a system and parameters with aleatory uncertainty are best represented with probability distributions. Examples of this kind of uncertainty are the results of rolling dice or radioactive decay.
Epistemic
Epistemic uncertainty is uncertainty that results from lack of information that we could theoretically know but don’t currently have access to. Thus, epistemic uncertainty could conceivably be reduced by gathering the right information but often isn’t due to the expense or difficulty of doing so. Examples of this kind of uncertainty include batch material properties, manufactured dimensions, and load profiles.
Common Sources of Uncertainty in Simulation and Testing
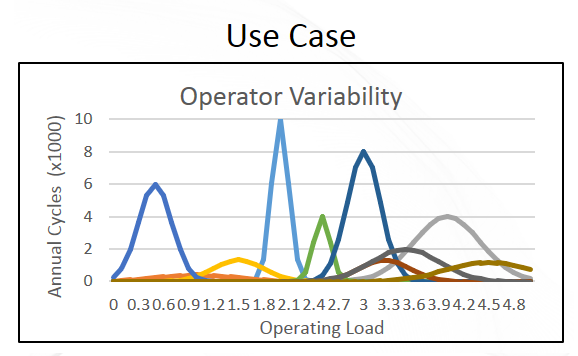Figure 2: Uncertain ScenariosUncertainties in simulation and testing appear in boundary conditions, initial conditions, system parameters, and in the systems, models, and calculations themselves. These uncertainties may be described in four categories: uncertain inputs, model form and parameter uncertainty, computational and numerical errors, and physical testing uncertainty.
Uncertain Inputs
Any system input including initial conditions, boundary conditions, and transient forcing functions may be subject to uncertainty. These inputs may vary in large, recordable, but unknown ways. This is often the case with operating conditions, design geometries and configurations, loading profiles, weather, and human operator inputs. Uncertain inputs may also be theoretically constant or follow known relationships but have some inherent uncertainty. This is often the case with measured inputs, manufacturing tolerance, and material property variations.
Modeling Form and Parameter Uncertainty
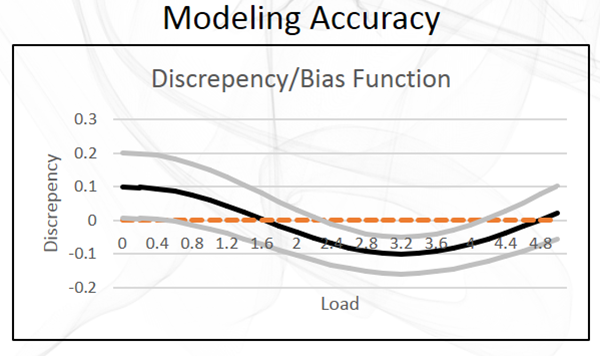Figure 3: Discrepancy FunctionAll models are approximations of reality. Modeling uncertainty is the result of errors, assumptions, and approximations made when choosing the model. This can be further broken down into model form uncertainty, i.e. uncertainty about the models ability to capture the relevant system behaviors, and parameter uncertainty, i.e. uncertainty about parameters within the model.
Using gravity as an example, the Newtonian model of gravity had errors in the model form which were fixed by general relativity. Thus, there is model form uncertainty in the predictions made using the Newtonian model of gravity. The parameters of both of these models, such as gravitational acceleration, are also subject to uncertainty and error. This uncertainty is often the result of errors in measurements or estimations of physical properties and can be reduced by using calibration to adjust the relevant parameters as more information becomes available.
Computational and Numerical Uncertainty
In order to run simulations and solve many mathematical models, it is necessary to simplify or approximate the underlying equations, introducing computational errors such as truncation and convergence error. For the same system and model, these errors vary between different numerical solvers and are dependent on the approximations and settings employed in each solver. Further numerical errors are introduced by the limitations of machine precision and rounding errors inherent in digital systems.
Uncertainty in Physical Testing
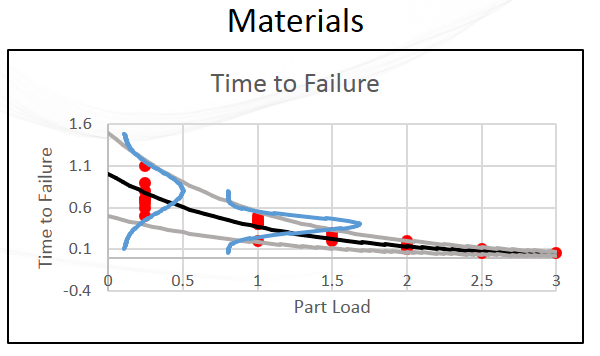Figure 4: Test VariationIn physical testing, uncertainty arises from uncontrolled or unknown inputs, measurement errors, aleatoric phenomena, and limitations in the design and implementation of tests, such as maximum resolution and special averaging. The presence of these uncertainties results in noisy experimental data and necessitates replication and reproduction in scientific experiments in order to reduce the effects of uncertainty on the desired measurement.
