SmartUQ offers a suite of specialized space-filling designs, an assortment of state of the art Design of Experiments (DOEs), and several unique patent-pending DOEs for complex challenges. We understand you have two main concerns when it comes to experimental design: getting enough data to accurately represent the system being sampled and controlling costs by reducing the number of samples.
Our state of the art DOEs ensure sufficient sampling while reducing the number of points required. Our proprietary DOEs go further, using information from previously sampled points to determine where the next samples should be taken to give you the data you need to move forward. You can even think outside the box by subsampling from large observational data sets. Plus, SmartUQ’s flexible DOE generation tools let you tailor your sampling to your specific needs.
One thing is certain, when you choose SmartUQ software to design DOEs, you will have more accurate and comprehensive results with significantly fewer runs, which saves both time and money.
Designs of Experiments (DOEs) are systematic sampling patterns that are used to conduct experiments to determine cause and effect relationships between inputs and outputs. Without a DOE that ensures sufficient information is gathered from the right experiments, it may be difficult or impossible to meet the test's objectives. If you conduct a simulation or testing experiment using sampling patterns which rely on the intuition of the experimenter or simulation user, it can result in a lack of understanding of how inputs interact with each other, which could waste testing resources and lead to missed opportunities.
Using a multi-factorial design, where several factors are varied simultaneously, can help resolve these problems. It’s critical to assess not only the effects of individual factors, but also how various pairs or combinations of factors may interact with one another to change output values.
Factorial DOEs provide robust information gathering capabilities but they often require taking more samples, at greater expense, than are truly necessary for determining cause and effect relationships in highly non-linear systems. Modern space-filling designs are often the most efficient DOEs for simulations and complex physical experiments with highly non-linear responses.
Space-filling designs, such as Latin hypercube designs and optimal Latin hypercube designs, sample a series of representative input configurations evenly distributed to fill the design space. Research shows this type of DOE minimizes the number of runs while maximizing the potential learning gained from each simulation. Thus, space-filling designs offer high accuracy while reducing the total number of sampling points.
Sequential DOEs use multiple DOEs, each optimized to fill gaps in the previous sampling pattern. This process can be repeated to increase emulator accuracy, helping minimize the total simulation time by only running the simulations necessary to achieve the desired level of accuracy. This DOE also allows new options for combining multi-fidelity simulations. Low-fidelity simulations can be used to generate an emulator and to quickly explore a design space. To ensure accuracy, the emulator can be calibrated using a smaller sampling of high-fidelity simulations. It is also possible to use this DOE to strategically run simulations and increase emulator accuracy as computational resources become available.
Example
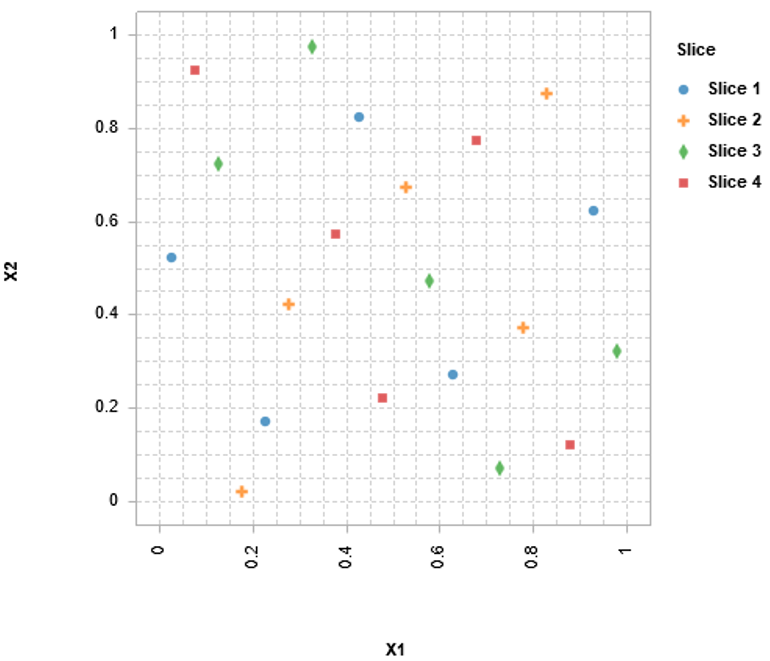
 Sequential DOE
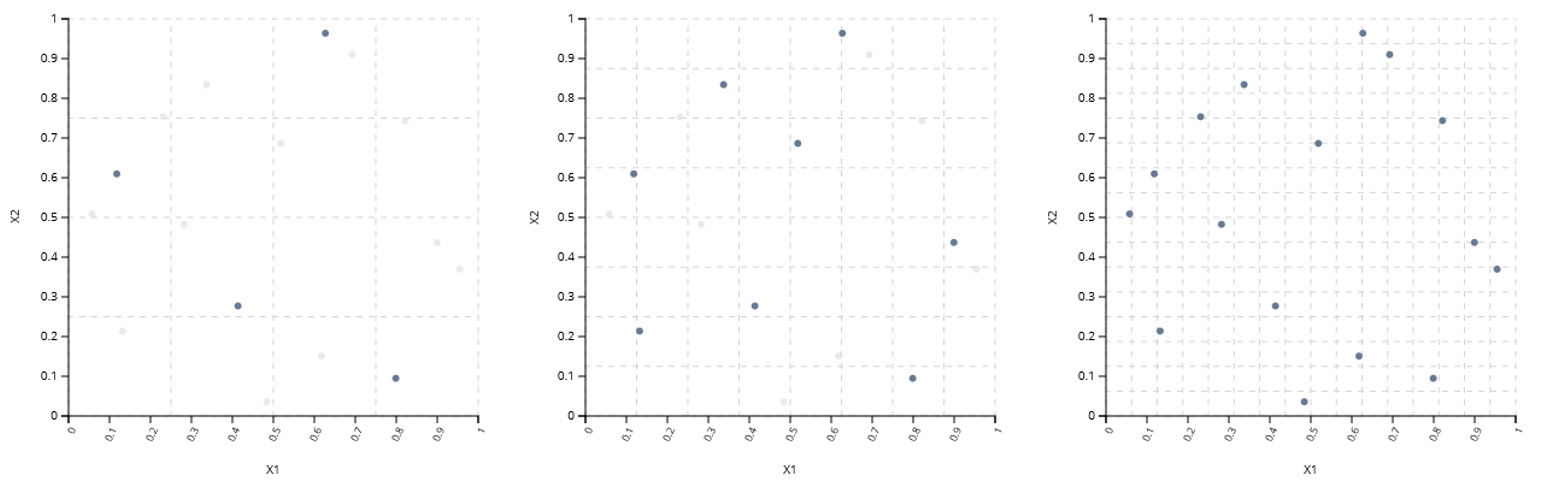
Sequential DOEIn parallel DOEs, the sampling points are divided into separate parallel batches. This is particularly helpful when varying a mixture of continuous and discrete inputs: each batch can handle a separate level of discrete inputs. It is also possible to support multiple discrete inputs by building each batch such that it is composed of smaller parallel DOEs.
These DOEs are also useful for dividing computational and experimental work between multiple groups. For computer experiments, being able to divide the computational load of the full experiment among larger groups of computing devices can yield a significant reduction in clock time.
Example
 Parallel DOE
Parallel DOE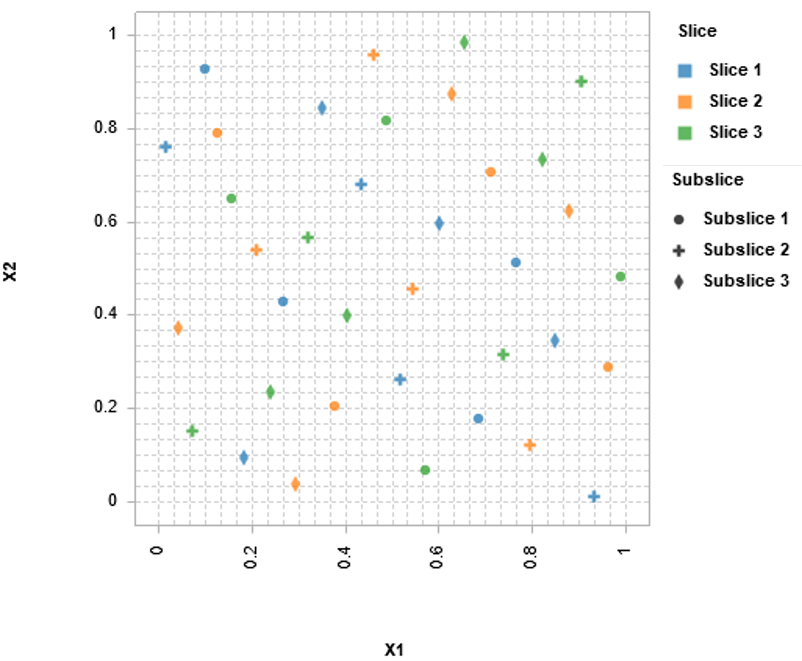 Doubly Parallel DOE
Doubly Parallel DOEi
Adaptive Design allows the user to increase the accuracy of a fitted emulator (surrogate model, meta-model) by adaptively adding more points to the DOE used to create the emulator. In this process, an emulator is created from an existing DOE and the associated results data. This emulator is then used to determine where the next simulation run should be added in order to increase the accuracy of the emulator. This process can be repeated until the desired level of fitting accuracy is achieved.
Example
A test surface, shown here, with several difficult-to-fit features was emulated by our algorithms using two methods: a one-shot optimal Latin hypercube design and our Adaptive DOE.
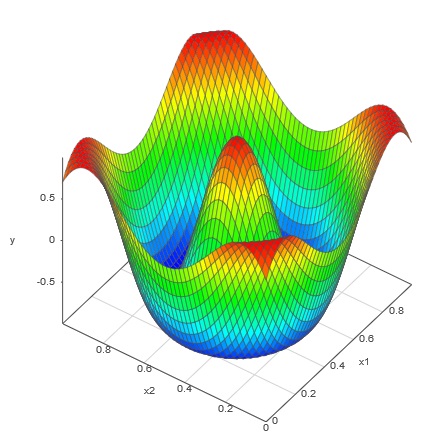 Test surface
Test surface
The first DOE was a one-shot optimal Latin hypercube design. The emulator generated with this DOE yielded the model surface shown below.
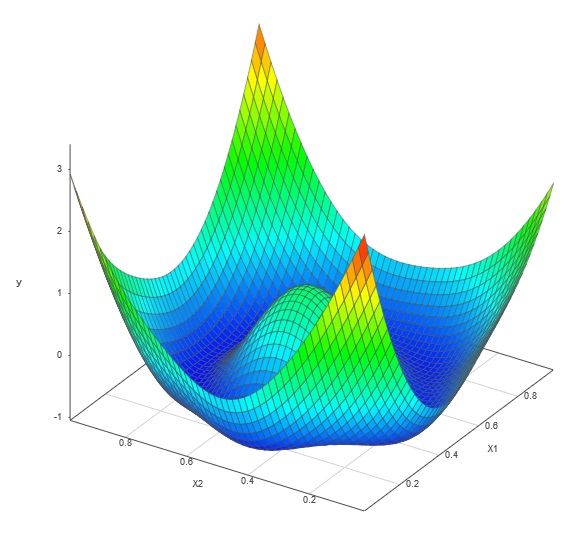 One-shot optimal LHD
One-shot optimal LHD
The second DOE was our proprietary Adaptive DOE. Starting with an initial 20-point optimal LHD, SmartUQ’s adaptive design feature added five points to the design space, one by one. Each point targets specific areas of the design space chosen by our algorithms based on the previous emulator. This approach resulted in a much more accurate model, reducing error by an order of magnitude while using the same number of simulation runs.
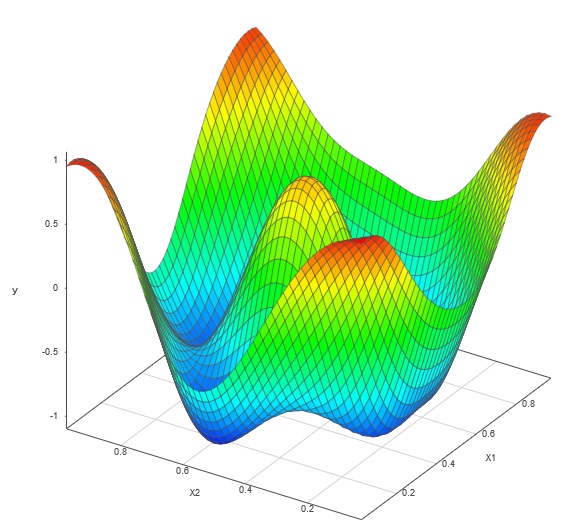 Adaptive DOE
Adaptive DOE
Design Augmentation allows the user to generate a DOE that combines with an existing DOE in such a way that the new points maximize the space-filling properties of the combined DOE. In practice, it is sometimes undesirable or infeasible to run all of the design points necessary for a large DOE in one simulation series. It is common to have existing DOEs from previous design space explorations, optimization procedures, and previous product development cycles. These DOEs might not have good space-filling properties but still contain valuable information. Design Augmentation is useful for determining the optimal simulation runs required to maximize the information that can be learned from a given number of new simulation runs while also taking advantage of previously collected data.
Design augmentation is different from Adaptive Design: In Design Augmentation the optimal points are generated based only on the properties of the existing DOE itself. Thus the new points are blind to the simulation results. In Adaptive Design, the optimal points are generated based on an emulator created using the previous simulation results as well as the properties of the DOE. Design Augmentation is more robust than Adaptive Design because the former is model free and works for simulations with any number of responses. Design Augmentation and Adaptive Design are both useful complimentary tools and the user should decide between these two options based on the properties of the specific case being studied.
Example
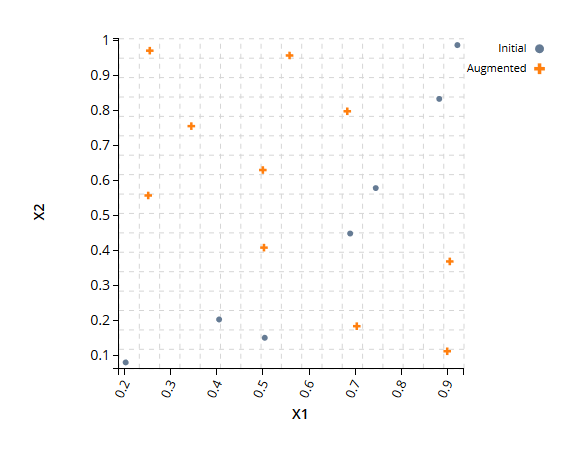 Augmented DOE
Augmented DOE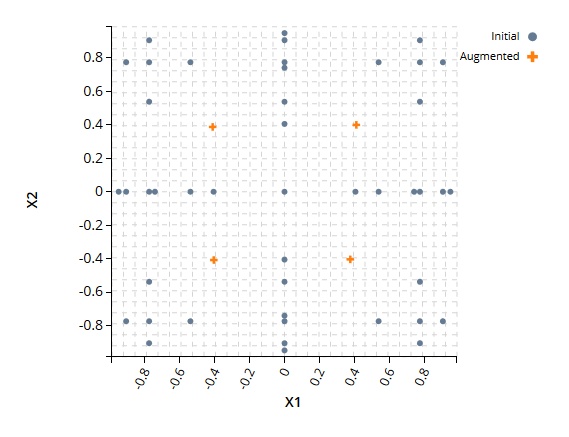 Sparse Grid
Sparse GridDOEs are typically used to collect new data from a system. In many cases, sufficient data has already been collected. Often in these scenarios, the data collected has been accumulated over long periods of time, and there is enough data that analysis is simply intractable. For example, health monitoring data from sensors on fielded components may capture live data continuously over the entire operating life of the component. SmartUQ’s data sampling tools can divide the data to mimic a space-filling DOE consisting of subsets of the full data set. Unlike DOEs which are developed before data collection, data sampling, such as subsampling and sliced sampling, takes existing input-output data pairs and selects the points that will represent the design space well.