Using a combination of proprietary adaptive DOEs and our breakthrough emulators, statistical optimization rapidly evaluates the design space and makes predictions about promising regions.
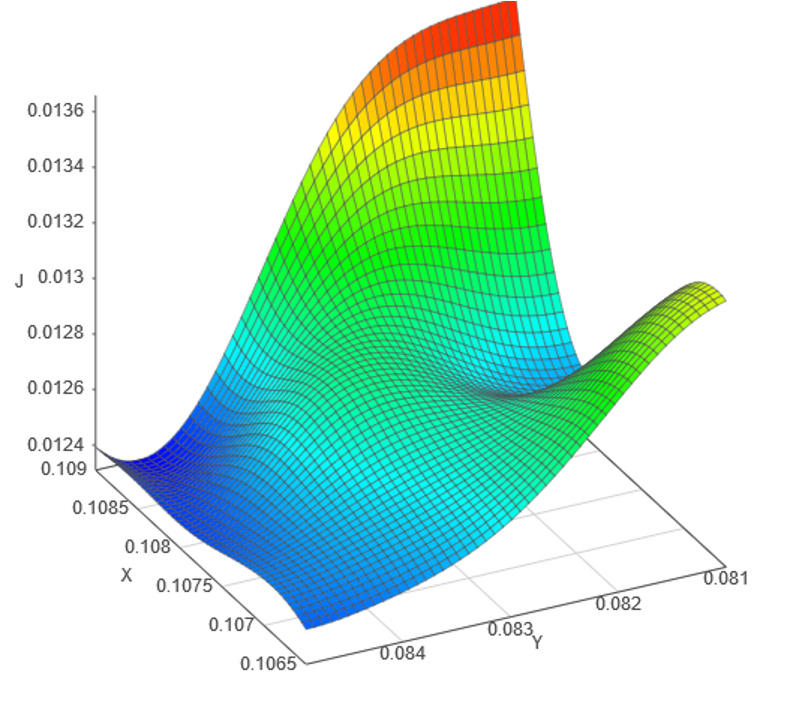
Statistical optimization works well with both low and high-dimensional problems. Our software minimizes the number of simulation runs required to get optimal results for a wide variety of problems and is capable of handling a large number of input and output types including binary and discrete, multiple constraints, and optimization with multiple goals.
With statistical optimization in SmartUQ, you can use an iterative DOE based sampling technique to improve knowledge of both the entire design space and regions likely to contain optimal points. Running sampling DOEs in parallel batches, instead of running single points in sequence, allows full use of computing resources and can deliver answers hundreds of times faster.
As an added benefit, significant savings can be achieved by using the same system evaluations for finding optimums as well as for analytics and UQ analysis of the optimization results. Not only can you explore optimal regions of the design space, you can determine how sensitive optimums are to changes in input parameters and whether variations around optimal points might lead to unexpected or undesirable behavior such as constraint violations.
Combinations of statistical optimization and search based optimization functions, such as genetic algorithms, can be used to take advantage of the best properties of both.
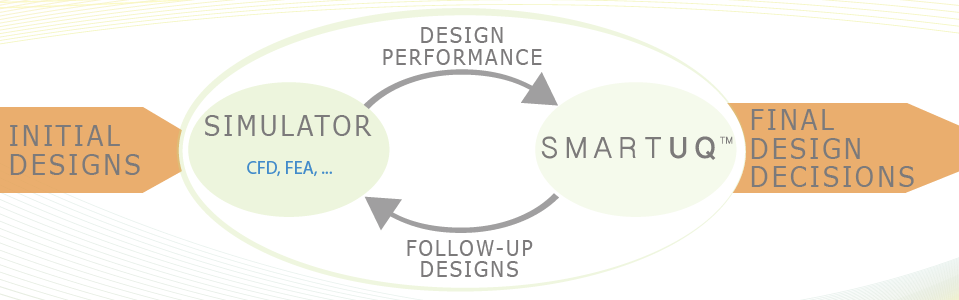Figure 1: Statistical Optimization Flow Chart Optimization under uncertainty is the process of optimizing a system's outputs when some or all of the inputs are uncertain. Rather than optimizing to find the best point for a single set of conditions, it is necessary to focus on identifying points that do well under a range of conditions and analysis of the behavior of the system around these optimal values. Without investigating the behavior around the optimal design point, it is difficult to avoid unstable optima that can result in undesirable behavior given normal variation in the final product.
For example, when optimizing the efficiency of a jet engine, it is necessary to consider the uncertainty in material properties, manufactured dimensions, and operating conditions of the actual system. Because of the uncertainty in the actual engine, it will likely operate near but not at the optimal design point. If the goal is to optimize for maximum efficiency while ensuring that the engine doesn’t violate pollution emission requirements, it is necessary to understand the engine behavior around the optimal design point. This helps ensure that, for the known uncertainties in the design inputs, the engine efficiency is always acceptable and the pollution requirements are never violated.
Emulator based optimization is the application of optimization algorithms to an emulator, taking advantage of the extremely fast prediction speeds to exhaustively cover the design space. Relying on our high-quality emulation technologies, SmartUQ has a built in optimization library capable of handling high dimensional problems with mixed continuous and categorical inputs, as well as multiple objectives, and constraints on inputs and outputs. With SmartUQ, the use of emulators as light weight stand-ins for complex systems can result in significant decreases in both the number of system evaluations and the clock time required to get solutions.
As with statistical optimization, once the emulators are constructed, they provide additional value in understanding the underlying system behavior and properties of the optimal points.
