The use of simulations to displace physical tests has become essential in accelerating analysis and reducing the cost of research and design. However, simulation results may be different from reality and it is critical to use statistical calibration and model validation to make the best use of limited test data in grounding models. The potential to reduce design cycle time and costs savings by ensuring that simulations are as close to reality as possible have never been greater.
Model calibration is the process of tuning model calibration parameters so that the model is in better agreement with a set of experimental results. Without proper calibration the results of the model could be meaningless or even provide misinformation on its real world counterpart. Thus, accurate model calibration is widely regarded as a key step in establishing a simulation model with adequate reliability and it is often necessary to calibrate a model before any further study or analysis can be conducted.
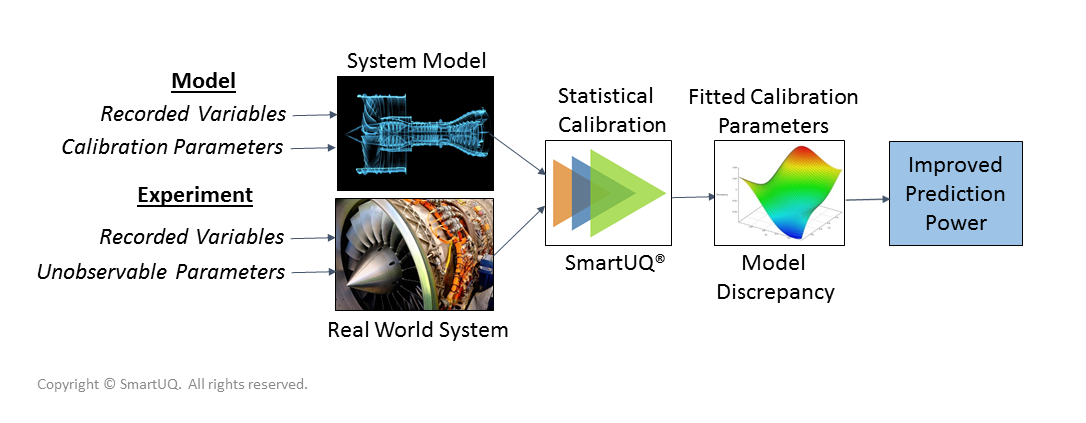Figure 1: Statistical calibration work flowThe work flow for statistical calibration is shown in the figure above. The calibration parameters are usually not directly measured in physical tests. These parameters may be physical properties, such as material and soil properties, manufactured dimensions, and engine operating points, which are difficult to measure or entirely non-physical properties of the model.
In thermal models of systems such as satellites buildings, it is often necessary to calibrate a variety of input parameters such as material properties, heat capacity of a component, refrigerant properties, convective heat transfer coefficients, and equipment or system performance. The outputs being matched can include temperatures, energy consumption, thermal expansion, heating rates, comfort levels, and equipment failure predictions. With so many possibilities, it’s easy to see why a simple, easy to use, effective calibration tool is a necessary.
The latest generation of simulation tools include highly detailed physics, greater complexity, and more parameters. Physical tests are also producing more and more complex data sets. Detailed instrument telemetry is common and handling it has become a question of big data analysis. The differences between simulation and testing results are an important component in uncertainty quantification analysis and these trends towards more complex models and large physical test data sets, present new challenges and opportunities in uncertainty quantification and statistical calibration.
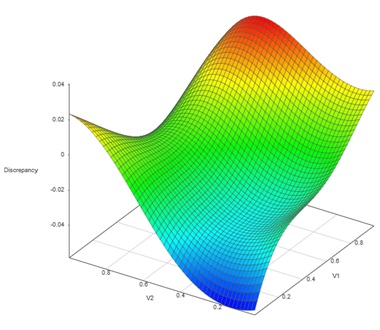Figure 2: Surface plot of the discrepancy prediction between a calibrated simulation model and a set of physical dataStatistical calibration has several important advantages. This method allows uncertainty in all aspects of the model, including uncertainty in the fitted calibration parameters. Statistical calibration also determines the discrepancy between the model and the observed data for the optimized calibration parameters. Determining model discrepancy is useful for highlighting inadequacies in models and necessary for model validation. The figure to the left shows a 2D surface plot of the model discrepancy between a simulation and physical data set.
SmartUQ’s statistical calibration feature can quickly and accurately tune models. Our easy to use interface allows you to calibrate almost any model including both low and high dimension models with univariate or multivariate outputs, and high-dimensional inputs. SmartUQ’s powerful algorithms simultaneously determines the discrepancy between the physical and simulation data and accurately calculates calibration parameters. Even better, all of the simulation runs required to calibrate the model can be run in parallel, drastically reducing clock time.
The accuracy of statistical calibration is tied to the physical and simulated data sets being used. SmartUQ provides a number of design of experiments generation tools designed to maximize the effectiveness and accuracy of statistical calibration. These tools can create optimized combinations physical and simulation designs of experiments or help with the placement of physical and simulation experiments in relation to existing data sets.
